理数探究の「数学」の事例が知りたい
探究学習の事例をお探しの先生へ。
2022年から本格的に始まる「探究学習」。理数探究の中で数学をどうやって教えたらいいかわからない･･･そういったお悩みをよくいただきます。
そこで本記事では「数学の探究学習事例」を調査してまとめました。
テーマやねらい、実践のプロセスや結果なども掲載しています。授業の参考にぜひお使いください。
【高校の探究担当の先生へ】
当メディアを運営する私たちStudy Valleyは「社会とつながる探究学習」を合言葉に、全国の高等学校様へ、探究スペシャリストによる探究支援と、社会とつながるICTツール「高校向け探究学習サービス『TimeTact』」を提供しています。
現在、探究に関する無料相談会を開催中です。探究へのICT活用や外部連携にご興味ある方、お気軽にご連絡下さい。ご予約はこちら（2024年3月現在、問い合わせが急増しております。ご希望の方はお早めにご連絡ください）。
【企業のCSR広報ご担当者様へ】
CSR広報活動の強い味方！
探究教育を通して、学校と繋がるさまざまなメリットを提供しています。
まずはお気軽に「教育CSRサービスページ」より資料をダウンロードください。
また無料相談も可能です。些細なご相談やご質問、お見積りなど、お気軽にご相談ください。
数学の探究学習のポイント
数学の探究学習を設計するうえで重要なポイントは大きく２つ。
・探究で何を学ぶのかを明確にする
・評価を明確にする
「総合的な探究の時間」が探究的な学びを身につけるのに主眼が置かれ、テーマや課題に自由度があるのに対し、教科の探究は、探究的な方法で「教科に関する知識や考え方」を身に付けることも期待されます。
探究を通じて、生徒が教科の知識や考え方を身に付けられるようにデザインしておく必要があります。
またペーパーテストと違い、成果だけでなく探究のプロセスも評価の対象になるのが探究学習です。探究のプロセスを評価する方法を決めておくことも重要です。
事例をご覧になる際も、これらのポイントを踏まえて見ていただく良いかと思います！ それでは、理数探究（数学）の事例を紹介していきます。
【解説あり】高校数学の探究学習事例５つを紹介【理数探究】
１．ラーメン屋の待ち時間を、数学・情報の横断で探究
「待ち」をキーワードに「渋滞」「インターネットの高速化」「ラーメン店」など身近な題材を、数学と情報で探究する実践です。
| テーマ | 数学と情報の横断的探究学習 |
|---|---|
| 学習期間 | 10～16時間 |
| 実施校 | 公立高校 |
| 対象学年 | ３年生 |
学習のねらい
問いへの探究を通じて、研究者の態度の育成を目的とした、世界探究パラダイムに基づいている「SRP（Study and Research Paths）」の可能性を探る。
課題・実施の流れなど
「待ち」をキーワードに、以下3つの問いを設定。
①渋滞に巻き込まれるとどれくらいの時間を損する？
②インターネットの高速化によって待ち時間はどれくらい減少したのか？
③ラーメン店の客の待ち時間を減らすにはどうすれば良いか？
これらの問いに対して
・授業説明・プレ探究（１時間）
・グループ活動（２～５時間）
・発表資料の作成（６～７時間）
・発表（１時間）
というように分割して活動を行ないました。 未習の知識についてはあらかじめ授業を行い、それ以外は教師は「探究サポーター」として生徒に新たな疑問を引き出すといった役割で接しました。
結果
ねらいとする、教科横断的な探究学習が実現したグループもありましたが、調べ学習で止まってしまうグループも見られました。
原因として、教科横断であるがゆえに「数学（情報）を使わなくてもよい」という意識が生じ、調べ学習に終わってしまった可能性や、適切な問いがたてられなかったことなどが推測されます。
ポイント
身近な題材を用いて、一見数学に結びつかない内容から、学習を深めている例。 伴走者として寄り添いつつ、途中で未習の範囲が出てきたときには必要に応じて講義を行うなど、先生が柔軟に役割を変化させ対応しているところもポイントです。
詳細：高等学校における数学と情報の教科横断的な探究型学習に関する研究
２．現代数学に挑戦！フィボナッチ数列を探究する
「畳」という身近な題材を入口に、「数列」「整数の性質」を発展させ、現代数学のフィボナッチ数列に触れてもらうという探究事例です。
| テーマ | 数列、整数の性質、フィボナッチ数列 |
|---|---|
| 学習期間 | １日（40分） |
学習のねらい
① 学力によらず、全ての生徒に数学の有用性を伝え、興味・関心を促す
② 現物実験を取り入れ、高校数学と現代数学のつながりを実感し、数学への探究心を育む
③ 認知プロセスの外化を促す協同学習を行うことによって、数学を探究する姿勢を養う
課題・実施の流れなど
「n畳の部屋（２×nの長方形）に畳を敷く。このとき、畳の敷き方は何通りあるか」という課題をきっかけにフィボナッチ数列に挑戦。畳のカードを用意し、手を動かしながらグループで取り組みました。
ステップ１（５分）：問題１「四畳の部屋に畳を敷く。このとき、畳の敷き方は何通りありますか」という問題に、カードを使った現物実験で取り組ませる
ステップ２（10分）：問題２「n畳の畳の敷き方は何通りありますか」という問題に取り組み「Fn=Fn-1+Fn-2」という式を推測させる
ステップ３（15分）：問題３として「なぜ、畳のひき方にFn=Fn-1+ Fn-2という関係性があるのか」という問題に取り組む
ステップ４（10分）：現代数学についての講義
結果
「数学への関心・興味」「数学の有用性」「実験の有用性」「共同効用因子」「反個人志向因子」「反互恵懸念因子」の６種類の因子、それぞれでデータをとったところ、全体で数学の有用性に対する意識が向上した結果が得られました。
ポイント
「勉強が何の役に立つの？」とはよく聞かれる問いです。数学は特に概念的で、生活や社会との結びつきを意識しにくい教科ではないでしょうか。
しかし、難しい学びでも、普段の生活に結びついていることを実感してもらうことで意欲的に取り組んでもらえることがわかる好例です。
３．オランダの数学コンテストに挑む？！渋滞を数学で探究する
オランダで行われている国際数学コンテストの問題を使用した探究事例です。
| テーマ | RMEアプローチ 国際数学コンテストの課題を通じた探究的な学習 |
|---|---|
| 実施校 | 金沢大学附属高校 |
学習のねらい
生徒がグローバルな社会課題に関心を持ち、協働しながら、複合的な視点で事象を捉えて問題を見出して解決するとともに、解決の過程や結果を実際の状況に照らして吟味し、一定の解決策を提案できる力を育成すること。
課題・実施の流れなど
課題は「ラッシュアワーの時間帯の総混雑量を求める」など、現実社会に起こりうる現象を扱うものです。
学習は、オランダのRME（Realistic Mathematics Education。ユトレヒト大学フロイデンタール研究所による）というアプローチに着目して設計され、大きく以下の３つの活動が実施されました。
①高校生向けのチームコンテストMath A-limpiad（エーリンピアド。国際数学コンテスト）の課題による総合的な探究活動の試み
②Mascilプロジェクト（EUの数理教育プロジェクト）で開発された教科横断的モジュールを活かした既設教科の指導内容と授業の改善
③Cito（オランダ教育測定研究所）が作成した全国共通試験問題を活用した課外での自主的な探究活動の実施
①、②では、実際に使われた予想問題を使ってグループワークを行ないました。
結果
授業実践後のアンケートによると、
・生徒はおおむね興味を持って取り組むことができた
・これまで取り組んできた数学の問題とずいぶん異なっているため、多くの生徒が難しく感じた
という結果が得られました。 扱った数学問題は難しいものでしたが、筆者は以下のことが得られたと述べています。
・長文英語読解や現実事象を分析しながら数学的課題を見つけること
・グラフや式を読んで事象を解釈したりする、といった行為を通して、多角的に考えたり、要点を簡潔に表現する力をつけた
・数学の有用性や共同的な問題解決の良さも感得することができた
ポイント
現実社会の問題をテーマとすることで、生徒は学習を自分ごとと捉え、意欲的に取り組みやすくなります。
それだけではなく、日常の現象を数学的にとらえ定式化したり、数学的な視点から事象を解釈したりする力を身につけていくのではないでしょうか。
ここから紹介する２つは実践事例ではなく、授業開発段階のものですが、シンプルで応用性が高いと考えられるものなので、ご紹介します。
４．多角形の直角の個数に関する探究授業開発
探究事例が少ない、図形の性質をテーマにした探究学習の授業開発例です。予備知識がなくても取り組めて、応用性の高い内容です。
| テーマ | 数学A・図形の性質、多角形の直角の個数に関する性質 |
|---|
学習のねらい
数学Aの「図形の性質」を通じて統合的な考え方、発展的な考え方などの数学的な考え方を育成することを目指す。 そのために生徒自らが、
図形の性質等を予想 →予想の真偽を証明 →振り返って吟味 or 別証明
という一連のサイクルを通して探究活動を行えるようにする。
課題・実施の流れなど
多角形の直角の個数に関する性質を考察することを全体の流れとして設計。 三角形からｎ角形の直角の個数の性質を、凸多角形の場合と凹多角形の場合で探究、証明する授業開発を行い、多くの図形を示し、視覚的にもわかりやすいものとなるように作成されました。
結果
授業開発の結果、以下の理由で探究活動を促す価値のある教材という結果が得られました。
・直角は小学２年生から扱う単元だが、その後は扱われことがなく、生徒にとって目新しい学習である
・予備知識を必要としないので、取り組みやすい
・発展・一般化が容易である
・生徒に苦手意識を持たれやすい「背理法」による論証が使われるので、論証能力をより高めることが期待できる。また、別の証明方法を考えるきっかけにもなると考えられる。
５．ペットボトルロケットの飛行実験を教材とした探究授業開発
ペットボトルロケットを実際に製作して実験を行うことで、二次関数について探究する授業例です。
| テーマ | 水ロケット（ペットボトルロケット）の飛行実験、二次関数 |
|---|---|
| 学習期間 | 合計11.5時間 |
| 実施校 | 高校１年生 |
学習のねらい
数学Ⅰにおいて水ロケットの飛行実験を教材とし、自主的な学習を促し数学の良さを認識できるようにする。
課題・実施の流れなど
ロケットの打ち上げ角度、水ロケット内の気圧や水量などを課題とし、数学Ⅰ・Aの学習内容との関連性を検討しました。
結果
指導計画案とメリットを以下のように整理しました。
指導計画
・課題の設定（30分）
・実験計画の作成（30分）
・水ロケットの制作（２時間）
・飛行実験（２時間）
・結果の考察・発表準備（1.5時間）
・発表会・発展課題の設定（1.5時間）
・発展課題の解決（1.5時間）
メリット
・二次関数を活用した探究が可能であること
・多様な課題を設定でき、発展的な学習に繋げられること
・多変数関数の学習を視野に入れた教材としても活用可能であること
ポイント
身近にある素材を使い、実験を通じて学習できるテーマです。さらに
・遠くに飛ばすには？
・高く飛ばすには？
・飛行時間を長くするには？
・角度と飛距離の関係
・気圧と飛距離の関係
・軌跡は？
など、多くの課題設定が可能で、角度、気圧、水量など多変数関数の学習を視野に入れた学習としても利用できる教材です。
無料ダウンロードOK！探究テーマ発見に役立つワークシート一式！
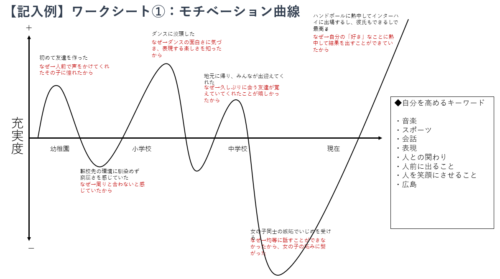弊社StudyValleyでは、生徒が興味関心に基づく探究テーマを見つけるためのワークシート（マンダラート（マンダラチャート）など）を、探究学習でお困りの学校の先生方に無料配布しております。 以下よりダウンロードしていただき、ぜひ探究学習活動にお役立てください。
【高校の探究担当の先生へ】
当メディアを運営する私たちStudy Valleyは「社会とつながる探究学習」を合言葉に、全国の高等学校様へ、探究スペシャリストによる探究支援と、社会とつながるICTツール「高校向け探究学習サービス『TimeTact』」を提供しています。
現在、探究に関する無料相談会を開催中です。探究へのICT活用や外部連携にご興味ある方、お気軽にご連絡下さい。ご予約はこちら（2024年3月現在、問い合わせが急増しております。ご希望の方はお早めにご連絡ください）。
【企業のCSR広報ご担当者様へ】
CSR広報活動の強い味方！
探究教育を通して、学校と繋がるさまざまなメリットを提供しています。
まずはお気軽に「教育CSRサービスページ」より資料をダウンロードください。
また無料相談も可能です。些細なご相談やご質問、お見積りなど、お気軽にご相談ください。
【この記事の監修者】
田中 悠樹｜株式会社Study Valley代表
東京大学大学院卒業後、ゴールドマンサックス証券→リクルートホールディングスに入社。同社にて様々な企業への投資を経験する中で、日本の未来を変えるためには子どもたちへの教育の拡充が重要であると考え、2020年に株式会社Study Valleyを創業。
2020年、経済産業省主催の教育プラットフォームSTEAM ライブラリーの技術開発を担当。
2024年、経済産業省が主催する「イノベーション創出のための学びと社会連携推進に関する研究会」に委員として参加している。
